샘플 기반 최적 모션 플래닝 알고리즘을 정리한 논문입니다.(pdf파일)
Sampling-based Algorithms for Optimal Motion Planning
0. Abstract
PRM(Probabilistic RoadMaps)과 RRT(Rapidly-exploring Random Trees)와 같은 sampling-based path planning 알고리즘은 실제로 잘 실행되고 probabilistic completeness와 같은 이론적 보장을 가지고 있지만, the quality of the solution 분석에는 적은 노력을 기울였습니다.
따라서, 이 논문을 쓴 목적은 각 알고리즘의 cost of solution을 엄격하게 분석하는 것입니다.
대다수의 결과들이 거의 확실하게 최적의 해에 수렴하지 못한다는 것이고 이 논문에서 PRM, RRT 알고리즘을 소개함으로써 최적의 해에 도달함을 보여줍니다.
-
Keywords
Motion planning, optimal path planning, sampling-based algorithms, random geometric graphs
1. Introduction
패스 플래닝이 어떻게 발전해 왔는지 설명하고 있으며 당연히 이전 플래닝의 단점을 보완하는 플래닝 알고리즘일 것입니다.
샘플 기반 알고리즘의 가장 큰 장점은 고차원 환경에서 매우 효율적이라고 합니다.
1-1. Sampling-Based Algorithms
가장 영향력있는 샘플기반 알고리즘은 PRM과 RRT가 있습니다.
두 알고리즘 모두 확률적으로 완벽한 알고리즘입니다.
차이점을 설명하자면, PRM 알고리즘은 그래프를 구성하기 위해 multiple-query 방법을 쓰기 때문에 계산양이 많고 infeasible 할 수 있습니다.
또한, 장애물이 없는 환경에서 동작하고 환경이 바뀌거나 알 수 없을 때는 여러 query가 필요하지 않습니다.
반면에 RRT는 single-query 방법을 쓰고 환경이 복잡해도 풀 수가 있다고 합니다.
1-2. Optimal Motion Planning
quality of the solution은 정말 중요합니다.
예를 들어 패스의 최단 거리(최소 비용)를 구하는 것입니다.
기존 알고리즘(RRT)에 비용을 고려해 확장시킨 여러 방법들이 고안되었고 다른 접근 방식인 A* 알고리즘에 대해 설명합니다.
A* 알고리즘은 오직 그리드 환경에서 사용되며 고차원일 수록 그리드 수와 계산 시간이 기하급수적으로 증가하는 문제를 가지고 있습니다.
1-3. Statement of Contributions
PRM, PRM-star, RRT, RRT-star 알고리즘의 확률적으로 완벽한지, 최적화, 계산적으로 효율성을 아래의 표로 보여줍니다.
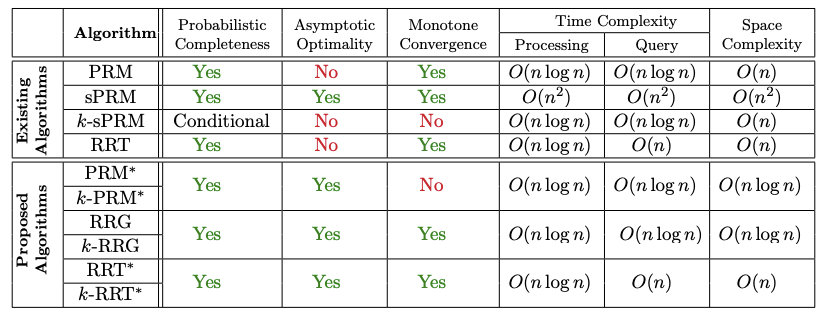
그래프에서 보듯이 RRT* 알고리즘이 가장 효율적이며 언제든지 모션 플래닝이 가능하다고 합니다.
1-4. Paper Organization
각 섹션에서 무엇을 설명할 것인지 간단하게 요약하는 문단입니다.
2. Preliminary Material
실현 가능하고 최적의 모션 계획 문제를 소개하고 랜덤 기하 그래프 이론의 몇가지 중요한 결과를 요약합니다.
이 부분은 생략하겠습니다.
3. Algorithms
먼저 PRM과 RRT 알고리즘을 소개하고 PRM-star, RRT-star 알고리즘을 소개합니다.
3-1. Primitive Procedures
-
Sampling
\(\left\{SampleFree_{i}(\omega)\right\}_{i\in\mathbb{N}_{0}} = \left\{Sample_{i}(\omega)\right\}_{i\in \mathbb{N}_{0}}\cap X_{free}\\\omega : sample\ point\) -
Nearest Neighbor
\(Nearest(G = (V, E), x) := argmin_{v∈V}\left \| x-v \right \|\) -
Near Vertices
\(Near(G = (V, E), x, r) := \left \{v ∈ V : v ∈ B_{x,r}\right \}\) -
Steering
\(Steer(x, y) := argmin_{z∈Bx,η} \left \| z-y \right \|\) -
Collision Test
\(CollisionFree(x, {x}') := [x, {x}' ] ⊂ X_{free}\)
3-2. Existing Algorithms
-
Probabilistic RoadMaps (PRM)

위의 수도 코드를 설명하겠습니다.
- V(vertexes), E(Edges)를 Null로 initialize 합니다.
- 0부터 n(limit)까지 반복을 하는 동안
- n개의 포인트를 랜덤 샘플링 하고
- r(이웃 반경) 이내의 모든 노드들을 찾고, 해당 노드들을 U에 저장합니다.
- 랜덤 샘플링한 포인트들 x_rand는 V에 저장합니다.
- U에 저장되어있는 노드(u)를 하나씩 꺼내 u와 x_rand 사이의 거리를 오름차순으로 정렬하고
- x_rand와 u가 연결되어 있지 않다면 : (V, E)를 통해 연결 여부 확인
- 장애물간의 충돌이 있는지 검사 후 E를 업데이트 합니다.
-
Rapidly-exploring Random Trees (RRT)

Rapidly-exploring random tree - Wikipedia
위의 수도 코드를 설명하겠습니다.
- 초기 상태를 V(vertex)에 포함시키고 E(edge)는 비어있도록 초기화 합니다.
- 1부터 n까지 반복을 하는 동안
- 랜덤한 포인트를 선택하고 (SampleFree)
- 선택한 랜덤 포인트와 그래프 안의 vertex들의 거리를 계산해서 가장 짧은 vertex를 선택합니다.(Nearest)
- 선택한 vertex point, random point의 unit vector를 구하고 η(step size)만큼 곱하여 random point를 더해 줍니다. unit_vector = x_nearest - x_rand x_new = x_nearest + unit_vector * η (η > 0, ||x_new|| ≤ η)
- x_new와 x_neareset 사이에 obstacleFree 인지 확인 하고,
- obstacleFree이면 V와 E를 업데이트 합니다.
- 반복문이 끝나면 Graph를 리턴합니다.
-
Optimal Probabilistic RoadMaps(PRM*)

기존의 PRM과 차이는 3번째 줄에 들어가는 r 입니다.
\(r := \gamma_{PRM}(log(n)/n)^{1/d}\)
위 식의 의미를 설명하자면, n은 노드 수이고, d는 차원 수입니다.
이웃 반경 r 노드 수가 많아지면 작아지고 log(n)에 비례한다는 것입니다.
따라서 노드 수가 많아지면 조밀한 그래프 형태의 로드맵이 됩니다.
좀 더 조밀한 경로가 생성되기 때문에 PRM보다 유연한 경로(직선 경로)가 만들어 집니다. -
Optimal RRT (RRT*)

기존의 RRT와의 다른 점은 Cost를 계산한다는 것과 PRM*에서 사용하는 r(이웃 반경)을 사용합니다.
x_rand에서 이웃 반경을 그려 이웃 반경 안에 노드(x_near)가 있으면 x_rand와 x_near를 이어주고 cost를 계산합니다.
cost를 최소화 하기 위한 노드를 선택하는 것이기 때문에 기존의 트리를 재구성하는 Rewire 단계를 거치게 됩니다.
따라서 샘플링을 많이 할 수록 RRT보다 유연한 경로가 만들어지며 최적의 경로를 보장하게 됩니다.