이번 시간에는 3차원 상의 회전 운동의 특성에 대해 살펴보겠습니다.

Chapter 2. Kinematics

2.2. Characteristics of Rotational Motion

2.2.1 Roll, Pitch and Yaw Notation

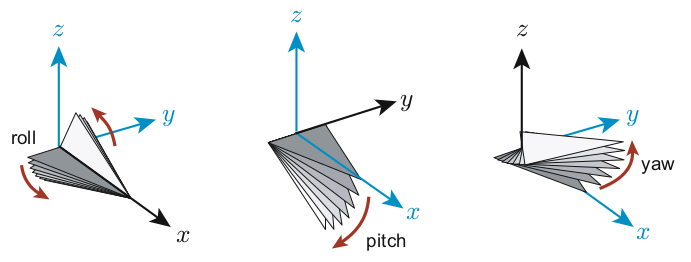
• x 축에 대하여 회전한 것을 roll

  y 축에 대하여 회전한 것을 pitch

  z 축에 대하여 회전한 것을 yaw

• 만약 점 p를 원점으로 부터 Roll, Pitch, Yaw 만큼 회전운동 시켜 p’을 얻었다면
  

  \[p'=R_z{\psi }R_y{\theta}R_x{\phi}p \\ p'=R_{rpy}{(\phi,\theta,\psi)}p\]

  
  

  이와 같이 쓸 수 있다.

• 3차원 공간에서 R을 이용하여 자세를 표현할 수 있으며 (Φ, θ, Ψ)을 Roll-Pitch-Yall 표기법 또는 Z-Y-X Eulner angles 이라고 부른다.

2.2.2 The Meaning of Rotation Matrices

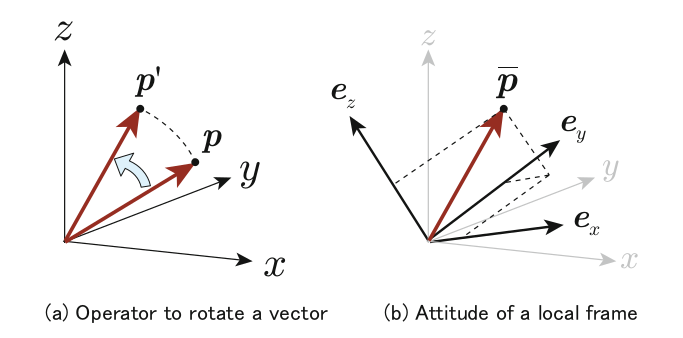
• p에서 p’으로 회전을 나타내는 방법으로 2가지 방법이 있다.

  (a)는 p와 p’의 프레임을 같게 보는 것이고 (b)는 local frame을 이용하는 것이다.

  (b)의 경우 R은 x, y, z 축의 unit 벡터로 표현한다.

2.2.3 Calculating the Inverse of a Rotation Matrix

local frame에서 자세를 표현한다고 가정했을 때

\[R^{T}\]

와 R의 곱을 계산해보면

\[R^{T}R = E \\ R^{T} = R^{-1}\]

어떤 행렬을 transpose 한 것과 inverse 한 것이 같다면 orthogonal matrices 이라고 부른다.

2.2.4 Angular Velocity Vector

TODO